Thématique de recherche
Les cyclones tropicaux représentent un enjeu majeur, à fort impact sociétal, dans un contexte de changement climatique. La montée des océans, combinée au risque de cyclones de plus en plus intenses soulignent la nécessité croissante d’une meilleure compréhension des mécanismes d’intensification des cyclones tropicaux. Dans mes recherches, je couvre ces questions tant sur le plan de l’intensification des cyclones (structure interne et interaction avec l’environnement) que sur celui de l’impact, en particulier en ce qui concerne les submersions associées à la houle cyclonique.
-
Dynamique des cyclones tropicaux (CT)
L'un des volets de mes recherches concerne la dynamique de formation de l'oeil des CT. Malgré son omniprésence dans les CT et son rôle clé dans l’intensification des CT, son mécanisme de formation fait toujours l’objet de débats dans la communauté. J’étudie également l’interaction des cyclones tropicaux avec leur environnement atmosphérique, en particulier l’effet du cisaillement vertical des vents. Mon approche s'appuie sur des modèles idéalisés et vise à extraire des mécanismes physiques. Photo : Ouragan Florence (2018), ISS, A. Gerst. -
Couplage océan-atmosphère et vagues extrêmes
Le couplage océan-atmosphère joue un rôle majeur dans la formation des CT. Un aspect de l'interaction CT-océan concerne la houle cyclonique générée lors du passage d'un cyclone. Les mécanismes menant aux vagues extrêmes, particulièrement dévastatrices, sont un sujet de recherche ouvert et actif. Notre travail s'appuie sur la modélisation numérique, les spectres d'énergie des vagues reconstruits à partir de l'instrument SWIM à bord du satellite CFOSAT et des données in situ. Photo: en immersion dans l'ouragan Sam, 2021 (Saildrone/NOAA). -
Impact des vagues sur les îles
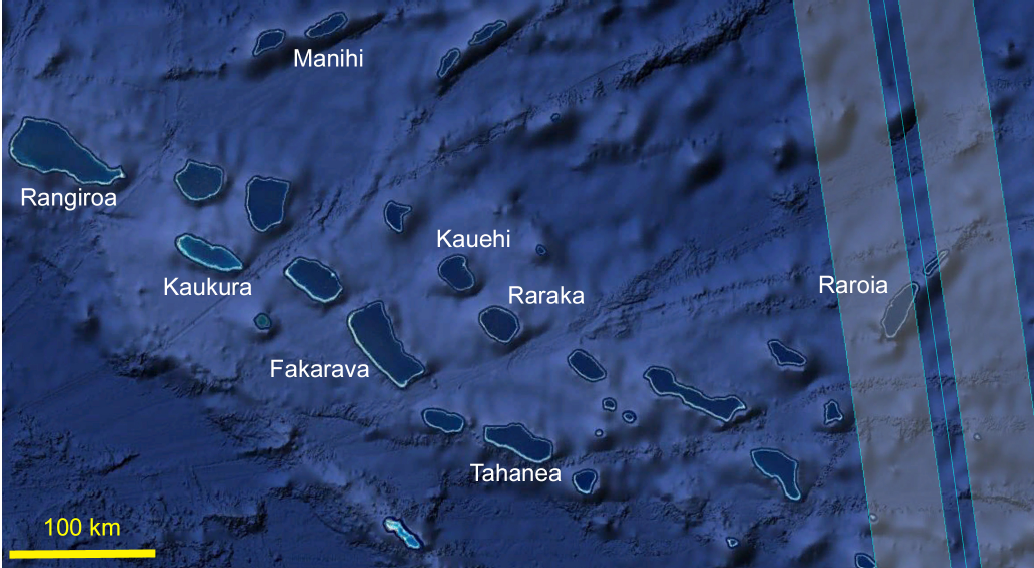Je m'intéresse également à l'impact des vagues extrêmes sur les îles hautes et les atolls. Les vagues venant du large et impactant une barrière récifale sont en partie dissipées et en partie transmises vers le lagon. L’étude de cette transmission et des vagues les plus dangereuses dans le cas d’un cyclone représente une question ouverte. L’étude des vagues transmises dans le lagon lors de fortes houles venant du large met notamment en évidence l’existence de modes de résonance à grande échelle, également appelés “seiches”. Figure: Rebouillat, Oruba et al, 2026.
Autres thèmes de recherche
J'ai auparavant étudié les mécanismes de formation et de déplacement des tempêtes
de moyennes latitudes ainsi que l'écoulement magnétodynamique (MHD) du métal
liquide du noyau de la Terre, à l'origine du champ magnétique terrestre.
-
Lois d'échelle pour les écoulements en rotation et la Géodynamo
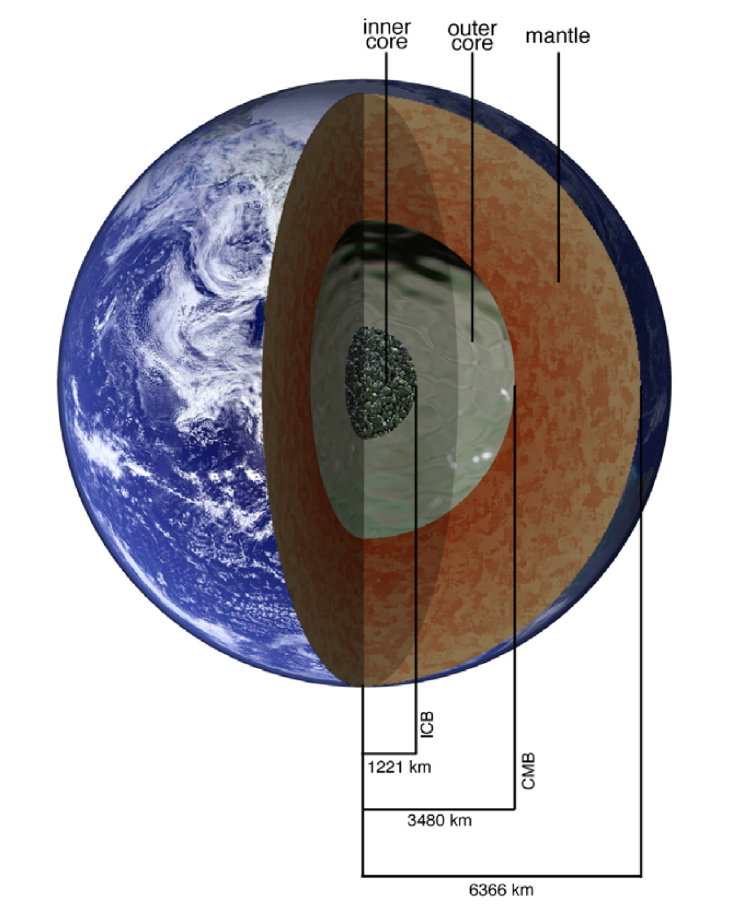L'écoulement des fluides géophysiques faiblement visqueux influencés par la rotation rapide de la Terre est caractérisé par des nombres sans dimension hors de portée des modèles numériques actuels. Ainsi, le métal liquide du noyau de la Terre est caractérisé par un nombre d’Ekman très faible E ~ 10-15. Les valeurs les plus faibles atteintes dans les modèles numériques sont de l’ordre de 10-6. Les résultats dépendent donc de E, et les lois d'échelle permettent d'extrapoler les quantités mesurées au noyau terrestre. J'ai travaillé sur ces lois d'échelle dans le cadre de l'étude de l'écoulement MHD du noyau externe de la Terre, qui génère la majeure partie du champ magnétique terrestre par effet dynamo. Figure: Robert and King (2013).Structures cycloniques des moyennes latitudes
Au début de ma carrière, je me suis intéressée aux tempêtes des moyennes latitudes, qui se développent au sein des courants jets d'altitude via le mécanisme d'instabilité barocline. J'ai étudié l'interaction non-linéaire entre le courant-jet et les dépressions afin de comprendre la croissance explosive de certaines tempêtes, comme Xynthia en février 2010. Mon travail s'appuyait sur un modèle quasi-géostrophique à deux couches dans l'approximation du plan beta. Image : Tempête Goretti (2025), Meteo-France.